故事背景(雾)

这周在为之工作室的分享会上讲了一发DFS入门知识，(似乎)效果还不错，于是想着拿出来更一发博客吧。也算是给想要了解DFS的同学的一份不是那么完美的教程喵。

什么是DFS

DFS(Deepth First Search),也就是深度优先搜索，是一种图论中的搜索算法，它遵循的最基本的策略就是去尽可能“深”的去搜索地图。

说的通俗一点，就是一条道走到黑，直到走不通了就往回走，直到走到目的地或者走完整个连通图。

举个例子：

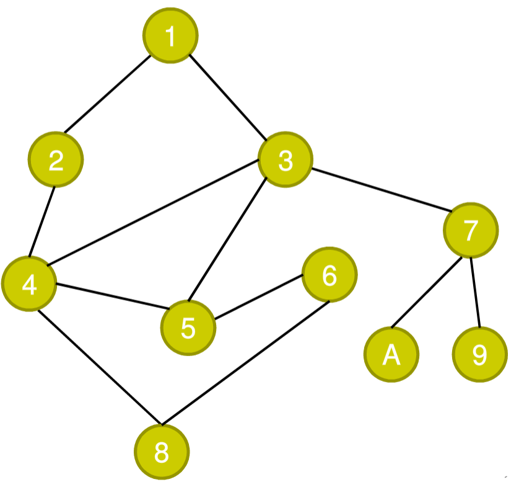
假设我们的目的是从1号点走到8号点，也就是说，完美要利用深度优先搜索的方法，从一号点开始，直到找到8号点为止。那么我们首先来明确一下深度优先搜索的策略：

从起点开始，随便选择一个子节点向下搜索，对于每一个节点，再随便选择它的子节点向下搜索，直到没有子节点为止。每到达一个节点，就标记该节点，直到全部节点都被标记或者到达目的地为止。
注意：这里我们强调了要随便选一个子节点向下搜索，也就是从直观上讲，我们的搜索过程和我们的运气有一定的关系。

首先有一个欧洲人开始进行搜索:
欧皇选择节点的方式是 1 -> 2 -> 4 -> 8，也就是一次就选到了正确道路。

之后轮到BB酱选择道路了：
不幸的是，因为BB酱是一个非洲人，他在一开始选取的时候没有选择2号点而是3号点，那么他的选择方案可能是这样的：
1->3->7->9 => 7-> A => 3 ->4 -> 8 (=>表示回退)
也就是说，BB酱在搜索的过程中，先沿着一条不正确的道路走到头，在倒回去找其他可能的走法，直到最终费尽千辛万苦走到终点为止。

小结

通过刚才的例子，相信大家对于深度优先搜索的最基本的搜索思路有了一个基本的认识，也就是一条道走到黑的思想。那么我们又会出现一个问题，当我们的地图不是联通的时候该怎么办呢？

另一个例子

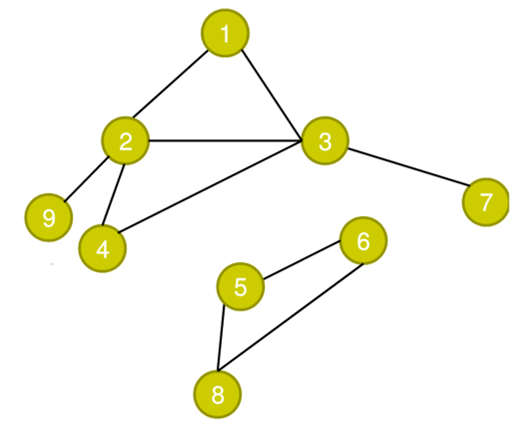
对于这张地图，我们用肉眼可以很清楚的看到，我们似乎并不能从1号点走到8号点，但是如果我们在深度优先搜索的过程中，又是怎样判断这个问题的呢？
这里先给出结论：
在得出无法到达的结论前，一定会把从1开始经过的点都走过一遍
我们的搜索过程可能是：
1->2->9=>2->4->3-7=>3=>4=>2=>1
和刚才一样，=>表示回退，那么我们可以看到，我们沿着所有可能的道路一直向下走，直到走遍了所有的道路，经过了所有的点，我们最终发现无法到达8号点。这种情况给了我们处理一类问题的一个思路，也就是在一整个地图上寻找所有连通图的个数的问题。

基础的原理问题讲到这里可以暂时告一段落了，这里我准备了4道例题，可以帮助我们由浅入深的具体理解深度优先搜索在题目中的实际应用。

---

例题时间

水洼数量问题(Lake counting) POJ2386/P1596

原题是英文，这里我直接给出题目大意

题目大意

我们用一个N*M(1<=N<=100;1<=M<=100)网格图表示。每个网格中有水(‘W’) 或是旱地(‘.’)。一个网格与其周围的八个网格相连，而一组相连的网格视为一个水坑。约翰想弄清楚他的田地已经形成了多少水坑。给出约翰田地的示意图，确定当中有多少水坑。

输入

第1行：两个空格隔开的整数：N 和 M 第2行到第N+1行：每行M个字符，每个字符是’W’或’.’，它们表示网格图中的一排。字符之间没有空格。

输出

一行：水坑的数量

Sample Input

10 12
W……..WW.
.WWW…..WWW
….WW…WW.
………WW.
………W..
..W……W..
.W.W…..WW.
W.W.W…..W.
.W.W……W.
..W…….W.

Sample Output

3

解题思路

这道题其实是一个遍历的问题，从找到一个W标记的水坑开始进行深度优先遍历，每找到一个相邻的W便把它标记成’.’，从而使得在主函数中每对一个点进行遍历，在图上该点所在的水坑都被覆盖成旱地，从而完成一次计数。
也就是说，我们在主函数中，先读入数据，对于地图上的每一个点，如果这个点表示水坑，我们就用dfs的方法从这个点开始，把该点所在的水坑填成旱地，之后让我们的计数器加一，这样就可以完成整道题的搜索过程。

代码实现

备注

这道题就是利用了之前提到的利用DFS的特性去寻找图上所有的连通图的思想，把每一个水洼都看成一个连通图，那么我们在寻找相连的过程时，就相当于找到了一个连通图，统计水洼个数的过程，就是统计这些连通图的个数。

---

部分和问题

题目描述

给定整数a1,a2…an，判断是否可以从中选出若干数，使他们的和恰好为k

Sample Input

5
1 2 4 5 6
13

Sample Output

YES

解题思路

这是一道很经典的深搜题目，对于每一次搜索，传入当前数字编号和当前选中的数字之和dfs(i,sum)，起始数据传入dfs(0,0)

在搜索过程中，如果传入的sum值等于k值，直接返回true，表示搜索完成。

对于当前传入的数字，有两种操作方式，即加在sum上和不加在sum上，因此也就引出两个搜索的分支
即dfs(i+1,sum)和dfs(i+1, sum+a[i])

值得注意的是，在我们进行深度优先搜索的过程中，一般情况下，我们进入一次搜索之后的第一件事情，就是去判断搜索是否已经结束，也就是说，对于这道题，我们需要的是先去判断我们是否已经走到看数据的末尾，再去判断是否已经达成sum==k的目标。
另一个重要的思想是，在搜索时，对于每一次传入的节点，我们需要去考虑对于这个节点在搜索有多少种可能的状态，对于这个题而言，对于当前位置的数字，它与加和sum的关系只有两种可能，也就是：
1.被加入sum上
2.不被加入sum上
因此对于我们传入的每一个节点，都会引出两条分支，即即dfs(i+1,sum)和dfs(i+1, sum+a[i])

代码实现

---

之前两个题目可以说是最基本的两种dfs的题型了，明确状态和搜索过程，写出来就可以了。接下来的这个题，我希望引入一个对于DFS来说极其重要的一个概念，也就是老生常谈的回溯方法

踩方格问题(百炼4103)

题目描述

有一个方格矩阵，矩阵边界在无穷远处。我们做如下假设：
a.每走一步时，只能从当前方格移动一格，走到某个相邻的方格上；
b.走过的格子立即塌陷无法再走第二次；
c.只能向北、东、西三个方向走；
请问：如果允许在方格矩阵上走n步，共有多少种不同的方案。2种走法只要有一步不一样，即被认为是不同的方案。

Input

允许在方格上行走的步数n(n <= 20)

Output

计算出的方案数量

Sample Input

2

Sample Output

7

基本思路

把问题放到矩阵中，问题抽象成从矩阵一点出发，每次只能向下或左或右移动一格。
对于每一个点枚举可能的状态，这里运用一点分治的思想，也就是把整体的问题分割成有限个小问题来解决，单就这个题而言，我们可以利用如下方式分解
分解问题：
从(i,j)出发，走N步的方案数，等于以下三项之和：
从(i+1,j)出发，走n-1步的方案数。前提：(i+1,j)没走过
从(i,j+1)出发，走n-1步的方案数。前提：(I,j+1)没走过
从(i,j-1)出发，走n-1步的方案数，前提：(I,j-1)没走过
也就是说，如果下一个格子之前没有走过，我们就可以把走N步的问题变成走N-1步的问题，剩下的要考虑的就是走N-1步应该怎么处理了。显而易见的是，整个过程是可以一步一步减少步数的，因此我们的搜索也就因此而成立。
注意
这里我们引入回溯的概念，我们已经知道，我们每到达一个点，要做的第一件事情就是把这个点的状态标记成已经走过。但是，在每次搜索结束后，我们必须回溯上一次搜索的结果，也就是把当前点再置成未经过的状态。
其实这个过程也不是很难理解，比如我们在某一次搜索过程中走过了(i,j)这个点，那么我们在这一次搜索中都不会再次经过这个点了。但是，当我们完成这一次的搜索，去进行下一次的搜索的时候，这个点必须要置成未被经过的状态，因为这个点在下次搜索仍然可能被经过。

小结

这道题比起之前的两道问题，可以说是真真正正的有了一些dfs的味道，这个题无论是对当前所在的每一个点的下一步可能的状态的讨论还是搜索之后的回溯，都是很有DFS感觉的问题，这道题作为一道新手入门级的DFS再好不过了。
那么至此，我们已经明确了DFS几乎所有的基础的知识点，也就是说，对于几乎所有的搜索题，只需要明确对于当前状态到下一状态有几种可能，每有一种可能就引出一个dfs分支，在完成一次搜索过程后回溯把之前标记过的点还原，就基本上可以从解决问题的角度完成任何一道搜索问题了。
但是，我们从刚才的题目里也能看出来，对于数据很大的地图，我们的递归的深度是非常深的，也就直接导致我们的运算时间爆炸式的增长。也就是说，虽然我们可以解决问题，但是可能会消耗大量的时间，无论是在日常应用还是ACM里，都不我们希望的结果。
碰巧我在分享会前整理PPT的当天，遇到了一道挺有意思的DFS问题，也就借着这道题分析一下一道真正的DFS问题的解决方案吧。

---

最终のBOSS战(雾)

POJ1724 Roads

题目描述

N cities named with numbers 1 … N are connected with one-way roads. Each road has two parameters associated with it : the road length and the toll that needs to be paid for the road (expressed in the number of coins).
Bob and Alice used to live in the city 1. After noticing that Alice was cheating in the card game they liked to play, Bob broke up with her and decided to move away – to the city N. He wants to get there as quickly as possible, but he is short on cash.
We want to help Bob to find the shortest path from the city 1 to the city N that he can afford with the amount of money he has.

Input

The first line of the input contains the integer K, 0 <= K <= 10000, maximum number of coins that Bob can spend on his way.
The second line contains the integer N, 2 <= N <= 100, the total number of cities.
The third line contains the integer R, 1 <= R <= 10000, the total number of roads.
Each of the following R lines describes one road by specifying integers S, D, L and T separated by single blank characters :
S is the source city, 1 <= S <= N
D is the destination city, 1 <= D <= N
L is the road length, 1 <= L <= 100
T is the toll (expressed in the number of coins), 0 <= T <=100
Notice that different roads may have the same source and destination cities.

Output

The first and the only line of the output should contain the total length of the shortest path from the city 1 to the city N whose total toll is less than or equal K coins.
If such path does not exist, only number -1 should be written to the output.

Sample Input

5
6
7
1 2 2 3
2 4 3 3
3 4 2 4
1 3 4 1
4 6 2 1
3 5 2 0
5 4 3 2

Sample Output

11

题目大意

N个城市，编号1到N。城市间有R条单向道路。
每条道路连接两个城市，有长度和过路费两个属性。
Bob有K块钱，他想从城市1走到城市N。问最短共需要走多长的路。如果到不了N，输出-1

2 <= N <=100
0 <= K <= 10000
1 <= R <= 10000
每条路的长度L, 1 <= L <= 100
每条路的过路费, 0 <= T <= 100

最直接的思路

我们拿到这个题，在我们熟悉DFS的基础上，我们不出意外应该都会有一个大致的思路了。也就是如下的思路：
从城市1开始进行dfs遍历整张地图，找到所有能够到N城市的走法，选择其中最短的一条。
相信各位只要好好看了上面的一大堆内容，这个思路应该是不难想到的，那么我们先把这个方法写出来。

使用的数据结构

主函数

相信大家应该都能读懂这个主函数，其实就是按照题目要求把数据读入，把每条路的信息存放在以起点为下标的vector里，也就是所谓的利用邻接表存放图的信息。把visited数组置成0，表示我们没有到过任何一个城市。给minlen一个很大的值，便于我们更新最小值。剩下的就是从1开始进行搜索，并在搜索结束后输出minlen了。
不理解vector的同学可以把它想象成一个二维数组，每一个G[i]都对应一个一维数组，这个一维数组的最小单元是一个Road结构体。G[s].push_back(r)的含义是在G[s]对应的数组里面添加一项r。
值得注意的一点是，在读入数据的时候去掉了自环，因为我们稍微想一下也就能明白，自环的存在只会让我们在这个城市绕上一圈，白白花费钱和路程，因此我们在输入的时候就直接去掉这种特殊情况。

DFS写法

存在的问题

这样的写法已经可以让我们解决这个问题，但是作为一道时间限制为1s的题目，这种写法离正确答案还有些遥远，事实上，这种写法到了数据量为几百的规模下，就可能需要几分钟甚至几十分钟才能计算出结果了。因此我们引入剪枝的概念。

剪枝

所谓的剪枝，就是我们在递归搜索的过程中人为的加入一些判断条件，从而减少一些不必要的运算。
对于这个题而言，如果在搜索过程中发现，假如当我们到达某一个点的时候，我们统计的当前所走的路径长度已经超过了之前找到的最短的路径长度，其实之后的运算都没有必要进行了，这会省下大量的运算。
所以我们在代码中加入剪枝的部分。

优化！优化！

经过刚才的剪枝，整个程序的运行时间会大幅的缩减，对于一些要跑很久的数据可能很快就能得出结果。大概估计一下的话，在1000到2000之间数据都可以通过测试，但是在数据量达到10000的条件下，这种剪枝又不够我们用了。
因此，对于本题而言，代码任然不够优化，在oj上，这道题给的时间限制是1秒，也就是说我们还需要对运算进行进一步的优化。
从直观上来看，我们可以想到，在不考虑路费的情况下，如果我们到达同一个点花费的路程比之前到达这个点所花费的最短路程要长，那么我们就应该认为这种方案一定不是最优解，应当舍弃。由此我们引入记忆化的概念。

记忆化

记忆化搜索，是指在搜索过程中记录一部分运算结果，从而对后续的运算进行最优性剪枝的操作。
对于这道题而言，我们刚刚讨论了不考虑路费的情况，那么如过把路费的因素考虑进去，我们要做怎样的记录呢？
其实和之前的方案非常类似：在花费相同的钱走并且到相同的位置的时候，如果此时的路径长度超过当前记录的最小值的时候，直接放弃。
于是我们有了如下的解决方案

1.引入一个二维数组minL[110][10005]在这个二维数组中，minL[k][m]表示走到城市k时，在总过路费为m的条件下，最优路径的长度。
2.在主函数中初始化该数组的值为无穷大
3.接着在最优化剪枝后加入新的操作，使得在花费相同的钱走到相同的位置的时候，如果此时的路径长度超过当前记录的最小值的时候，直接放弃。
4.若没有舍弃，则将新的数据写入该二维数组，为之后的操作提供基础。

第二次改写后的dfs函数如下

完成！

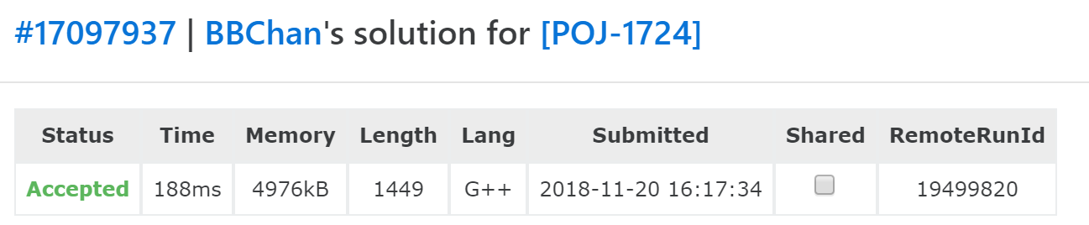
经过我们的努力之后，这一次的提交就可以通过这道题目。可以看到，经过我们的优化过程，程序运行时间由最初的超时到现在的188毫秒，可以说有了大幅度的提升，这也就是为什么说剪枝和记忆化在搜索过程中如此重要了。
最后附上正确的全部代码

小结

这道题算是一道正统的结合剪枝和记忆化搜索的深度优先搜索的题目，通过这道题我们也可以看到，剪枝和记忆化在整个搜索过程中起到的关键作用，相信各位看官如果能够一直看到这里，那么恭喜您！您对DFS已经有了一个基本的认识，也可以解决大部分的DFS问题了。

总结&后记

写博客好累喵。为了整理这篇文章又在图书馆坐了一个下午，不过感觉还是蛮不错的。DFS中涉及到的大部分问题都在这篇文章里多多少少的提到了一点，也不知各位看官是不是满意（虽然可能根本就没有看官QAQ）。人家真的尽力了嘤嘤嘤。毕竟我也是水平有限，也许还有些讲到周到甚至讲的不对的地方，也希望您能提出您的宝贵建议喵。