前言

又是两个多月没更新博客了，上个学期感觉忙忙碌碌的过得很快，这个假期时间比较长，且不论假期过完前途如何，不如趁这个假期多更新几篇文章来的实在。

这次的内容是属于机器学习基础知识的决策树相关的原理。有一说一，决策树在现在深度学习盛行的环境下，似乎没什么出境的机会，我其实也是在机器学习课上才真正了解到了这个算法。虽然用的人比较少，但是我觉得信息熵和信息增益的概念很有意思，这里就以一个简单的例子说明一下算法的原理吧。

算法原理

确定信息熵

针对输入的数据集，首先要求其信息熵，信息熵的定义如下：
\text{Ent}(D) = -\sum^{|y|}_{k=1}{p_k\times log_2p_k}
其中，D代表当前样本状态集合，P代表概率集合，p_k 表示当前样本集合D中第k类样本x_k所占比例，|y|表示类别个数。

易知，\text{Ent}(D)的值越小，D的纯度越高，样本的确定性越高。

确定信息增益

对于数据集中每一个属性a，需要确定该属性对于整个样本集D的信息增益，信息增益的定义如下：
\text{Gain}(D,a) = \text{Ent}(D) – \sum^V_{v=1}{\frac{|D^v|}{|D|}Ent(D^v)}
考虑到离散属性a的所有可能取值集合{a^1, a^2,\dots, a^V}，用a来进行划分，会产生V个分支节点，记D^V为第v个分支结点包含了D中所有在属性a上取值为a^v的样本，由此可确定出某一属性a的信息增益。

ID3算法

ID3算法的核心在于在决策树各个结点上应用信息增益准则选择信息增益最大，即信息熵下降速度最快的特征，利用递归的方法构建决策树，具体过程如下：

输入:训练集D = {(x_1,y_1), (x_2,y_2), \dots,(x_m,y_m)}

​ 属性集A = {a_1,a_2,\dots,a_d}

输出:决策树T:\text{TreeGenerate}(D,A)

STEP1: 若D中的所有样本都属于同一类C，则T 为单节点树，并将C作为该节点的类标记，返回T，否则转 STEP2；

STEP2: 计算D的信息熵D和每一种决策属性对应的信息增益\text{Gain}(D,a);

STEP3: 选择信息增益最大的属性a_p设为根节点，并根据a_p将数据集划分成v_p个子集{D^{a^1_p}, D^{a^2_p},\dots, D^{a^{v_p}_p}} ;

STEP4:令D = D^{a^j_p}, A = A – a_p，转到 STEP1.

问题求解

数据集D

序号	特征A	特征B	特征C	标记
1	0	1	1	0
2	1	1	1	0
3	0	0	0	0
4	1	1	0	1
5	0	1	0	1
6	1	0	1	1

求解D的信息熵

\begin{align}
\text{Ent}(D) =& -\sum^{|y|}_{k=1}{p_k\times log_2p_k}\\
=& -(\frac{3}{6}\times log_2{\frac{3}{6}}+\frac{3}{6}\times log_2{\frac{3}{6}})\\
=&1
\end{align}

求解每一个特征的信息增益

\end{align}

\begin{aligned}
\text{Gain}(D,B) =& \text{Ent}(D) – \sum^V_{v=1}{\frac{|D^v|}{|D|}\text{Ent}(D^v)}\\
=& \text{Ent}(D) – (\frac{2}{3}\times\text{Ent}(D^1) + \frac{1}{3}\times\text{Ent}(D^2))\\
=&1 – [\frac{2}{3}(-\frac{1}{2}log_2{\frac{1}{2}} -\frac{1}{2}log_2{\frac{1}{2}}) + \frac{1}{3}(-\frac{1}{2}log_2{\frac{1}{2}} -\frac{1}{2}log_2{\frac{1}{2}})]\\
=& 0.0
\end{aligned}

\begin{align}
\text{Gain}(D,C) =& \text{Ent}(D) – \sum^V_{v=1}{\frac{|D^v|}{|D|}\text{Ent}(D^v)}\\
=& \text{Ent}(D) – (\frac{1}{2}\times\text{Ent}(D^1) + \frac{1}{2}\times\text{Ent}(D^2))\\
=&1 – [\frac{1}{2}(-\frac{1}{3}log_2{\frac{1}{3}} -\frac{2}{3}log_2{\frac{2}{3}}) + \frac{1}{2}(-\frac{2}{3}log_2{\frac{2}{3}} -\frac{1}{3}log_2{\frac{1}{3}})]\\
=& 0.08170416594551044
\end{align}
$$

选择根节点，重新划分数据集

由上述求解结果可知，\text{Gain}(D,A) = \text{Gain}(D,C) > \text{Gain}(D,B)，因此可选择A特征或C特征值作为根节点构造决策树，不妨选择A节点为根节点。

此时，数据集被划分为两个部分D^{‘}_1, D^{‘}_2，分别对应序号{1, 3, 5}和{2, 4, 6}

递归求解决策树

对于获得的新的数据集D^{‘}_1, D^{‘}_2，分别进行上述信息增益运算，直至某一数据集的全部样本都属于同一类，最终构造出决策树。

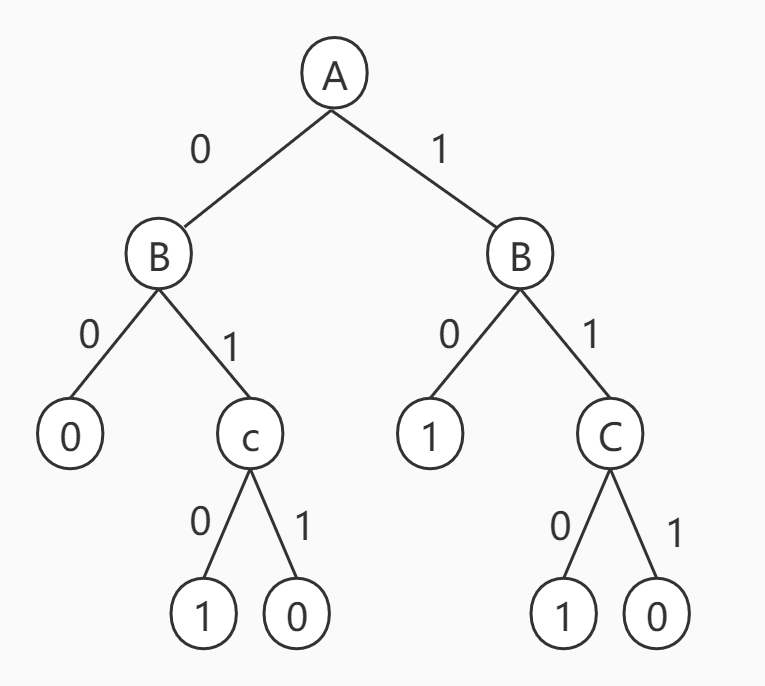
题目结果

构造出的决策树如下所示：

附录

计算信息熵的代码如下所示：

计算信息增益的代码如下所示：